Inżynier i Fizyk Medyczny 4/2017 vol. 6
223
artykuł
/
article
radioterapia
/
radiotherapy
Algorytmy ewolucyjne
a przybliżenie frontu Pareto
Algorytmy ewolucyjne zwykle nie zapewniają precyzyjnego
wyznaczenia frontu Pareto, ale pozwalają wskazać jego dobre
przybliżenie w rozsądnym czasie obliczeniowym. To jest walor
stanowiący o ich praktycznej przydatności: pozwalają szukać
rozwiązań przybliżonych dla problemów trudnych obliczenio-
wo, z wieloma zmiennymi decyzyjnymi. Żądanie ścisłego wyty-
czenia całego frontu Pareto byłoby obliczeniowo bardzo kosz-
towne, zwłaszcza w odniesieniu do zadań optymalizacyjnych
o wyższych wymiarach, a takie z reguły są rzeczywiste problemy
wielokryterialne. Precyzyjne wyznaczenie frontu Pareto jest dla
współczesnych komputerów nie lada wyzwaniem, ponieważ
w większości przypadków ów front nie posiada znanej struktury.
Aproksymacja (przybliżenie) frontu Pareto to problem, który
także sam w sobie ma naturę wielokryterialną. Algorytmy ewo-
lucyjne powinny prowadzić do takiego rozmieszczenia rozwią-
zań wzdłuż frontu Pareto, aby charakteryzowały je [17, 18]:
a)
zbieżność, czyli ukierunkowanie i minimalizacja odległości
wygenerowanych niezdominowanych rozwiązań do rzeczy-
wistego (ścisłego) frontu Pareto;
b)
różnorodność rozwiązań, czyli w miarę jednorodna dystry-
bucja rozwiązań; aproksymacja różnych obszarów frontu
Pareto;
c)
elitarność, czyli uniknięcie problemu tracenia danych (tj.
niezdominowanych rozwiązań) w trakcie optymalizacji;
strategia polegająca na kopiowaniu ustalonej liczby najlep-
szych rozwiązań do następnej generacji.
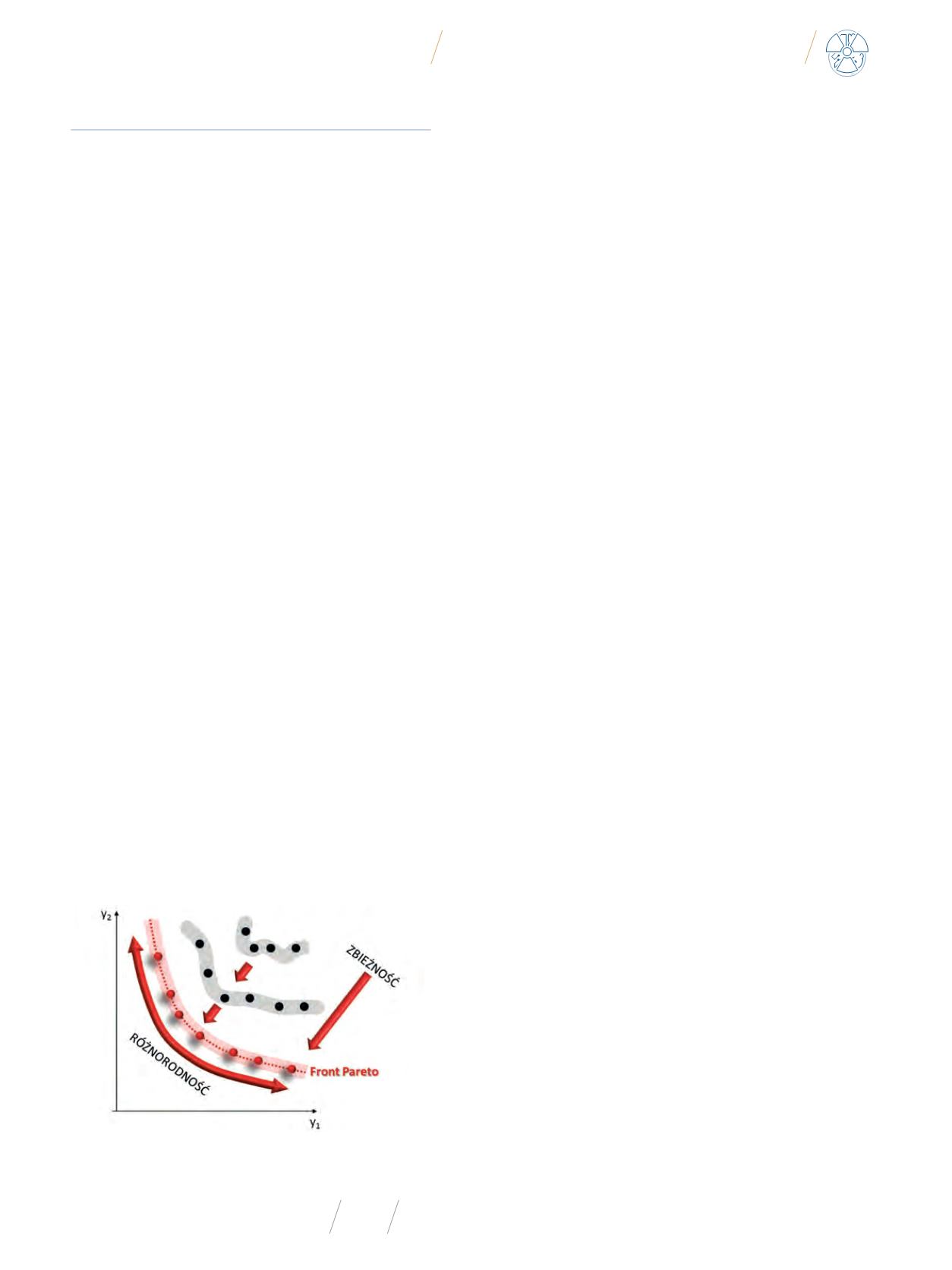
Jak z tego wynika, działanie MOEA powinno prowadzić do
znalezienia (wygenerowania) zbioru rozwiązań niezdominowa-
nych, o jak największym stopniu zbieżności do ścisłego frontu
Pareto, a jednocześnie zapewniających szeroką różnorodność
populacji (Rys. 8). Wygenerowany zbiór rozwiązań powinien być
możliwie mały, a przy tym jak najbardziej reprezentatywny.
Porównanie uzyskanych rozwiązań ułatwia często stosowa-
na wizualizacja frontu Pareto i nawigacja po nim. Należy jed-
nak zaznaczyć, że front lub powierzchnia Pareto daje się łatwo
wizualizować wtedy, gdy dane są tylko dwie funkcje kryterialne
(przestrzeń kryterialna jest dwuwymiarowa, dim
Y
= 2), nato-
miast problemy z wizualizacją rodzą się wówczas, gdy występują
więcej niż dwa kryteria.
Jak już powiedziano, działanie algorytmu ewolucyjnego
przebiega zgodnie z prawami doboru naturalnego i ewolucji.
Najpierw więc tworzona jest losowa populacja początkowa,
po czym tworzy się nowe populacje, wybierając z populacji po-
przedniej najlepsze osobniki, czyli rozwiązania (oceniając je za
pomocą funkcji celu). Wprowadziwszy operatory genetyczne,
generuje się następne pokolenia, a w każdym z nich wybierani
są osobnicy coraz lepsi wedle ustalonego układu kryteriów (ska-
larnych funkcji kryterialnych wchodzących w skład wektorowej
funkcji celu
f
) [10].
Uzyskane rozwiązania Pareto-optymalne (rozwiązania nie-
ulepszalne) matematycznie są równie dobre, a zatem mogą
być uznane za prawidłowe kompromisowe rozwiązania wielo-
kryterialnego problemu optymalizacyjnego. Problemem o nie
mniejszym znaczeniu niż przybliżenie frontu Pareto jest na-
stępnie wybór konkretnego rozwiązania ze zbioru rozwiązań
Pareto-optymalnych. Algorytmy MOEA i metody bazujące na
Pareto-optymalności są przykładem metod
a posteriori
włącza-
nia decydenta do procesu wybierania rozwiązania optymalnego
[13, 17]. W przypadku metod tej klasy decydent angażowany jest
w ostatniej fazie procesu decyzyjnego. Na tym etapie został mu
już dostarczony pełen obraz otrzymanych możliwych rozwiązań.
Wówczas podejmuje on ostateczną decyzję, które konkretne
rozwiązanie (konkretny kompromis) ze zbioru rozwiązań Pareto-
-optymalnych w danych warunkach będzie dla niego najbardziej
przydatne. A zatem rozwiązywanie wielokryterialnego problemu
optymalizacyjnego metodami
a posteriori
przebiega dwufazowo:
faza 1.: optymalizacja wielokryterialna
→
zastosowanie wy-
specjalizowanego algorytmu do uzyskania zbioru
Pareto-optymalnego,
faza 2.: podejmowanie decyzji
→
wybór przez decydenta kon-
kretnego rozwiązania kompromisowego ze zbioru roz-
wiązań Pareto-optymalnych.
Metody
a posteriori
stanowią najlepszą taktykę wyznaczania
rozwiązań problemów optymalizacji wielokryterialnej, ponie-
waż na etapie podejmowania przez decydenta ostatecznej de-
cyzji jest już zdefiniowany cały zbiór najlepszych niezdomino-
wanych rozwiązań. W procesie optymalizacji decydent został
zastąpiony matematycznym modelem wolnym od ustalanych
subiektywnie wag poszczególnych kryteriów oceny. Wadą tych
metod może być – paradoksalnie – przedstawienie decydento-
wi zbioru rozwiązań, który będzie na tyle duży, że jego rozmiar
uniemożliwi decydentowi podjęcie trafnej decyzji z powodu
zbyt wielu możliwych rozwiązań [4, 13].
W drugiej części artykułu zostanie zaprezentowany matema-
tyczny model optymalizacji w planowaniu IMRT, zaś w części
trzeciej praktyczne wykorzystanie przedstawionej teorii opty-
malizacji wielokryterialnej w kilku kluczowych dla planowania
leczenia kwestiach.
Rys. 8
Kluczowe kwestie w poszukiwaniach wielokryterialnych prowadzących do
przybliżenia frontu (powierzchni) Pareto
Źródło: Opracowano na podstawie [17].


