vol. 6 4/2017 Inżynier i Fizyk Medyczny
218
artykuł
\
article
radioterapia
\
radiotherapy
Charakteryzują się one tym, że optymalność w ich przypadku
rozumiana jest w szerszym sensie i oznacza, że każde rozwiąza-
nie z tego zbioru będzie się różniło, ale w pewnym sensie bę-
dzie optymalne. Dane rozwiązanie jest Pareto-optymalne, jeśli
nie jest możliwe znalezienie rozwiązania lepszego z uwagi na co
najmniej jedno kryterium oceny bez konieczności pogorszenia
pozostałych kryteriów [2-5].
Przedstawienie możliwości, jakie daje zastosowanie teorii
optymalizacji wielokryterialnej MCO w radioterapii i w planowa-
niu leczenia, wymaga poruszenia wielu zagadnień, co przekra-
cza ramy jednego artykułu. Zatem w tym tekście – stanowiącym
punkt wyjścia do dalszych omówień i analiz – zaprezentuję, opie-
rając się na odpowiedniej literaturze przedmiotu, fundament
koncepcji optymalizacji wielokryterialnej, tzn. jej podstawowy
aparat matematyczny przydatny fizykowi oraz niezbędną ter-
minologię, a następnie praktyczne wykorzystanie tej koncepcji
w kilku kluczowych dla planowania leczenia kwestiach.
Poszukiwanie optymalnych decyzji
w ujęciu matematycznym
Obecnie optymalizacja wielokryterialna (MCO) to szybko rozwi-
jający się obszar badawczy leżący na pograniczu matematyki i in-
formatyki. Jego jądro stanowi pojęcie
optymalizacji
rozumiane
jako poszukiwanie i wyznaczanie najlepszego rozwiązania pew-
nego problemu ze zbioru jego możliwych rozwiązań; formalnie
opisuje się je jako poszukiwanie ekstremum pewnej funkcji lub
funkcjonału. Rozwiązanie najlepsze, zatem optymalne, stanowi
albo minimum, albo maksimum jakiegoś wskaźnika jakości. Jest
więc rozwiązaniem, dla którego wartość funkcji celu jest najlep-
sza (min lub max) z punktu widzenia ustalonego kryterium oceny
lub układu kryteriów oceny [6-8].
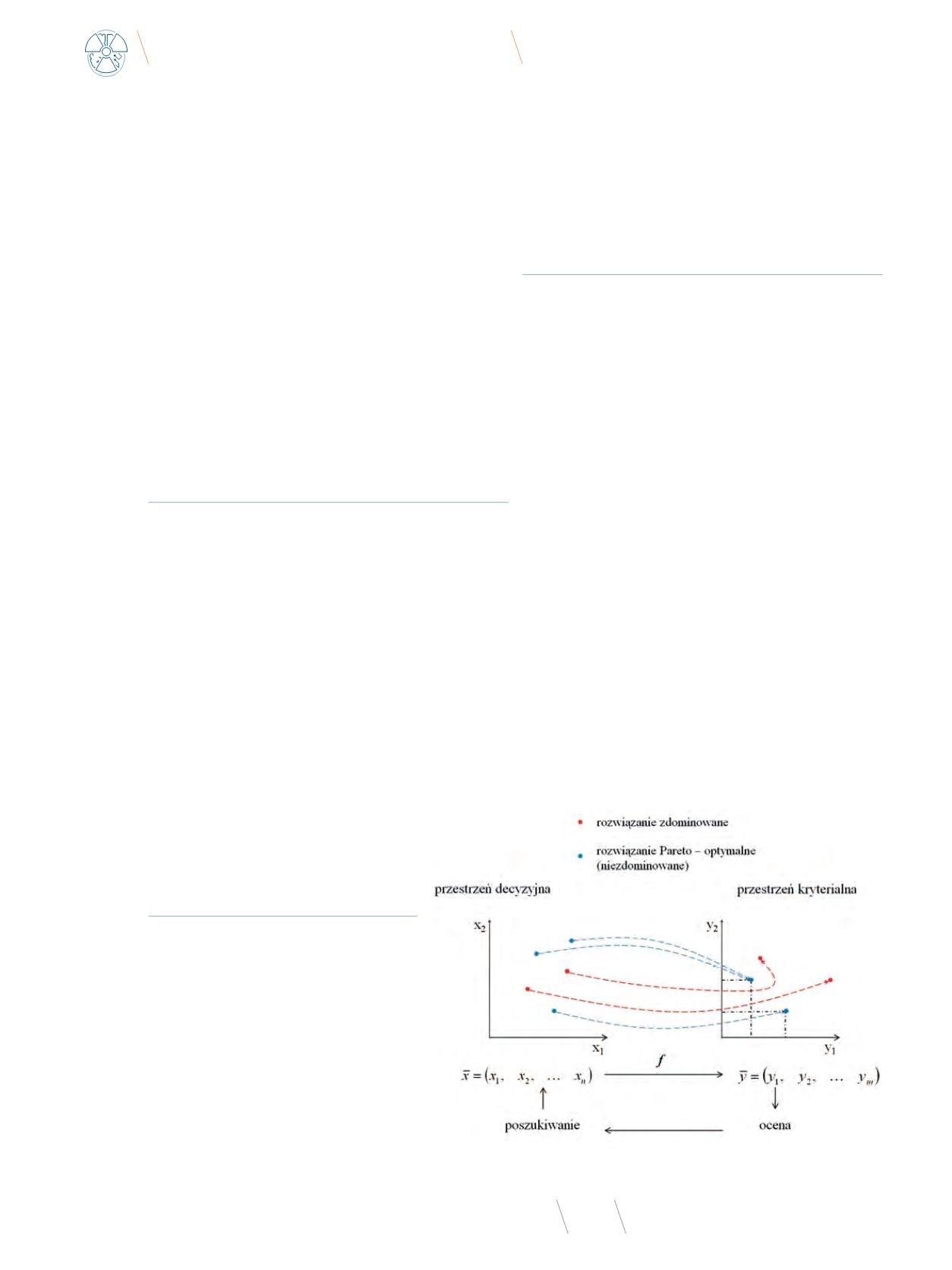
Zadanie optymalizacji wielokryterialnej może być rozważane
w dwóch przestrzeniach – przestrzeni decyzyjnej (przestrzeni de-
cyzji możliwych do podjęcia) oraz przestrzeni kryterialnej (prze-
strzeni ocen podejmowanych decyzji) [9].
Przestrzeń decyzyjna
X
=
n
i wektory zmiennych
decyzyjnych
Optymalizacyjne problemy decyzyjne matema-
tycznie definiowane są poprzez tzw. wektory
zmiennych decyzyjnych
x
= (
x
1
,
x
2
,...,
x
n
) będące
elementami n-wymiarowej, euklidesowej prze-
strzeni decyzyjnej
X
=
n
.
Wektory zmiennych decyzyjnych opisują
ex-
plicite
podjęte decyzje.
Na zmienne decyzyjne nałożony jest szereg
ograniczeń (w postaci układu równań i nierów-
ności), przez co mogą one przyjmować warto-
ści jedynie z określonego zbioru wartości do-
puszczalnych Ω
⊂
X
. Zatem wektor decyzyjny
x
będący rozwiązaniem problemu optymalizacyjnego nie może
być dowolny – musi należeć do zbioru decyzji (wektorów) do-
puszczalnych. W praktycznych (rzeczywistych) problemach
optymalizacyjnych ograniczenia te są z reguły wynikiem na przy-
kład ograniczonych możliwości fizycznych i technologicznych
realizacji pewnych decyzji [9-10].
Przestrzeń kryterialna
Y
=
m
i wektory
kryterialne oraz wektorowa funkcja celu
Ustalenie w problemie decyzyjnym, czy dane rozwiązanie jest
„złe”, „dobre” czy „najlepsze”, wymaga przede wszystkim zdefi-
niowania jakiejś miary, która pozwoli ocenić jakość podejmowa-
nych decyzji. W języku matematyki wskaźnikiem jakości podjętej
decyzji jest tzw.
funkcja celu
szacująca jakość konkretnego roz-
wiązania (wektora zmiennych decyzyjnych
x
) poprzez przypo-
rządkowanie mu tzw. wektora kryterialnego
y
w m-wymiarowej
euklidesowej przestrzeni kryterialnej
Y
=
m
.
W przypadku optymalizacji wielokryterialnej mamy do czynienia
z wektorową funkcją celu
f
= (
f
1
,
f
2
,...,
f
m
)
(1)
będącą przekształceniem (odwzorowaniem) n-wymiarowej
przestrzeni decyzyjnej
X
=
n
w m-wymiarową przestrzeń kryte-
rialną
Y
=
m
:
f
:
X
→
Y
f
:
n
→
m
(2)
Inaczej mówiąc, funkcja celu odwzorowuje zbiór Ω dopusz-
czalnych wektorów zmiennych decyzyjnych z przestrzeni de-
cyzyjnej
X
=
n
w zbiór Λ osiągalnych wektorów kryterialnych
w przestrzeni kryterialnej
Y
=
m
:
f
: Ω
→
Λ
(3)
Λ = {
y
∈
Y
:
y
=
f
(
x
),
x
∈
Ω}
(4).
Zatem zbiór Λ jest obrazem zbioru Ω poprzez wektorową funk-
cję celu
f
[9-10].
Rys. 1
Schematyczna ilustracja idei problemu optymalizacji wielokryterialnej
Źródło: Opracowano na podstawie [11].


