Inżynier i Fizyk Medyczny 4/2017 vol. 6
219
artykuł
/
article
radioterapia
/
radiotherapy
Innymi słowy, problem znalezienia najlepszego rozwiązania
– najlepszego wektora zmiennych decyzyjnych
x
(czyli podjęcia
najlepszych decyzji) – przenoszony jest do przestrzeni kryterialnej
i sprowadza się do poszukiwania najlepszego wektora lub wekto-
rów kryterialnych
y
w zbiorze Λ pod względem określonego ukła-
du kryteriów oceny, czyli skalarnych funkcji kryterialnych
f
1
,
f
2
,...,
f
m
będących składowymi wektorowej funkcji celu
f
, a także pojedyn-
czymi zmiennymi. Należy podkreślić, że wektorom różniącym się
wprzestrzeni decyzyjnej mogą być przyporządkowane jednakowe
wektory w przestrzeni kryterialnej (tj. różne decyzje prowadzą do
takich samych rezultatów). Wówczas takie wektory
x
są uważane
za jednakowo dobre z punktu widzenia funkcji celu [9-11].
Możemy teraz podać formalny, matematyczny zapis proble-
mu decyzyjnego, który zdefiniowany jako zadanie optymalizacji
wielokryterialnej sprowadza się do problemu znalezienia mini-
mum (lub maksimum)
1
wektorowej funkcji celu
f
nad zbiorem
Ω (czyli do znalezienia wektora
x
minimalizującego bądź maksy-
malizującego funkcję
f
) [6-10]:
min
{
f
(
x
):
x
∈
Ω}
min {
f
1
(
x
)
f
2
(
x
),...
f
m
(
x
):
x
∈
Ω}
(5),
gdzie:
a)
x
= (
x
1
,
x
2
,...,
x
n
) to wektor zmiennych decyzyjnych w n-wymiaro-
wej euklidesowej przestrzeni decyzyjnej
X
=
n
.
b) Ω
⊂
n
to niepusty zbiór dopuszczalnych wektorów zmien-
nych decyzyjnych w
X
, określany poprzez układ równań i nie-
równości nałożonych na te zmienne:
Ω = {
x
:
g
(
x
) ≤ 0,
h
(
x
) = 0}
g
j
:
n
→
,
j
= 1,...,
p
c
(6)
h
j
:
n
→
,
j
=
p
c
+1
,...,
p
c)
f
i
:
X
→
Y
,
i
= 1,...,
m
to
i
skalarnych składowych wektorowej
funkcji celu
f
. Każda ze skalarnych funkcji kryterialnych
f
i
re-
prezentuje konkretne kryterium decyzyjne.
d)
y
=
f
(
x
) = (
y
1
,
y
2
,...,
y
n
) to wektor kryterialny w m-wymiarowej
przestrzeni kryterialnej
Y
=
m
.
1
Zadanie minimalizacji można wyrazić jako problem maksymalizacji
przez przekształcenie
min
{
f
(
x
)} = –
max
{–
f
(
x
)}
Model preferencji, relacja dominacji
Proces rozwiązywania jakiegokolwiek problemu decyzyjnego
związany jest z koniecznością zastosowania pewnego modelu
preferencji, który umożliwia porównanie dwóch elementów
zbioru rozwiązań, a zatem dwóch rezultatów (dwóch różnych
decyzji), czyli dwóch wektorów kryterialnych
y
i
y
’
Podstawową formą modeli preferencji są modele oparte na
pojęciu
relacji
(określającej preferencje decydenta) zdefinio-
wanej w danym zbiorze. Relacja binarna (dwuargumentowa)
zdefiniowana na niepustym zbiorze Ω rozwiązań dopuszczal-
nych porównuje ze sobą pewne elementy tego zbioru. Model
preferencji precyzuje, że dla pewnych par elementów zbioru
określone jest, który z nich jest lepszy [2, 10, 12]. W ogólności
w procesie rozwiązywania wielokryterialnych problemów decy-
zyjnych można wyodrębnić cztery podstawowe fazy, na które
składają się [12-13]:
I.
Zdefiniowanie zbioru Ω (zbioru decyzji/rozwiązań dopusz-
czalnych) oraz ustalenie typu problemu decyzyjnego (czyli
określenia, czy proces rozwiązywania ma dotyczyć wybo-
ru „najlepszego” rozwiązania, znalezienia podzbioru „do-
brych” rozwiązań, czy może uporządkowania rozwiązań od
„najlepszego” do „najgorszego”).
II.
Sformułowanie kryteriów oceny rozwiązań.
III.
Modelowanie (synteza) globalnego modelu preferencji
decydenta.
IV.
Użycie tego modelu w zakresie konkretnych reguł
decyzyjnych.
Koronne znaczenie ma etap modelowania preferencji, ponie-
waż jest on bezpośrednio odpowiedzialny za to, że uzyskane roz-
wiązanie problemu decyzyjnego będzie pokrywało się z oczeki-
waniami decydenta.
I tak, w przypadku optymalizacji MCO uwzględniającej wiele
kryteriów relacją binarną definiującą rozwiązania „złe”, „dobre”
i „najlepsze” w zbiorze osiągalnych rozwiązań najczęściej jest
przechodnia relacja dominacji [10, 13].
Definicja
Rozwiązanie
x
(wektor zmiennych decyzyjnych powiązany
z wektorem kryterialnym
y
) dominuje rozwiązanie
x
’ (wektor
zmiennych decyzyjnych powiązany z wektorem kryterialnym
y
’)
x
x
’ wtedy i tylko wtedy, gdy wektory te spełniają następujące
warunki:
x
x
’
⇔
[
∀
i
∈
{1,...,
m
}:
y
i
=
f
i
(
x
) ≤
y
’
i
=
f
i
(
x
’)]
∧
[
∃
i
∈
{1,...,
m
}:
y
i
<
y
’
i
]
(7)
Innymi słowy: wektor (rozwiązanie)
x
dominuje inny wektor
(rozwiązanie)
x
’,
jeżeli jest przynajmniej tak samo dobry pod
względem wszystkich kryteriów (wszystkich skalarnych skła-
dowych funkcji celu) i lepszy ze względu na co najmniej jedno
kryterium.
Relacja dominacji umożliwiająca porównywanie elemen-
tów zbioru dopuszczalnych wektorów zmiennych decyzyjnych,
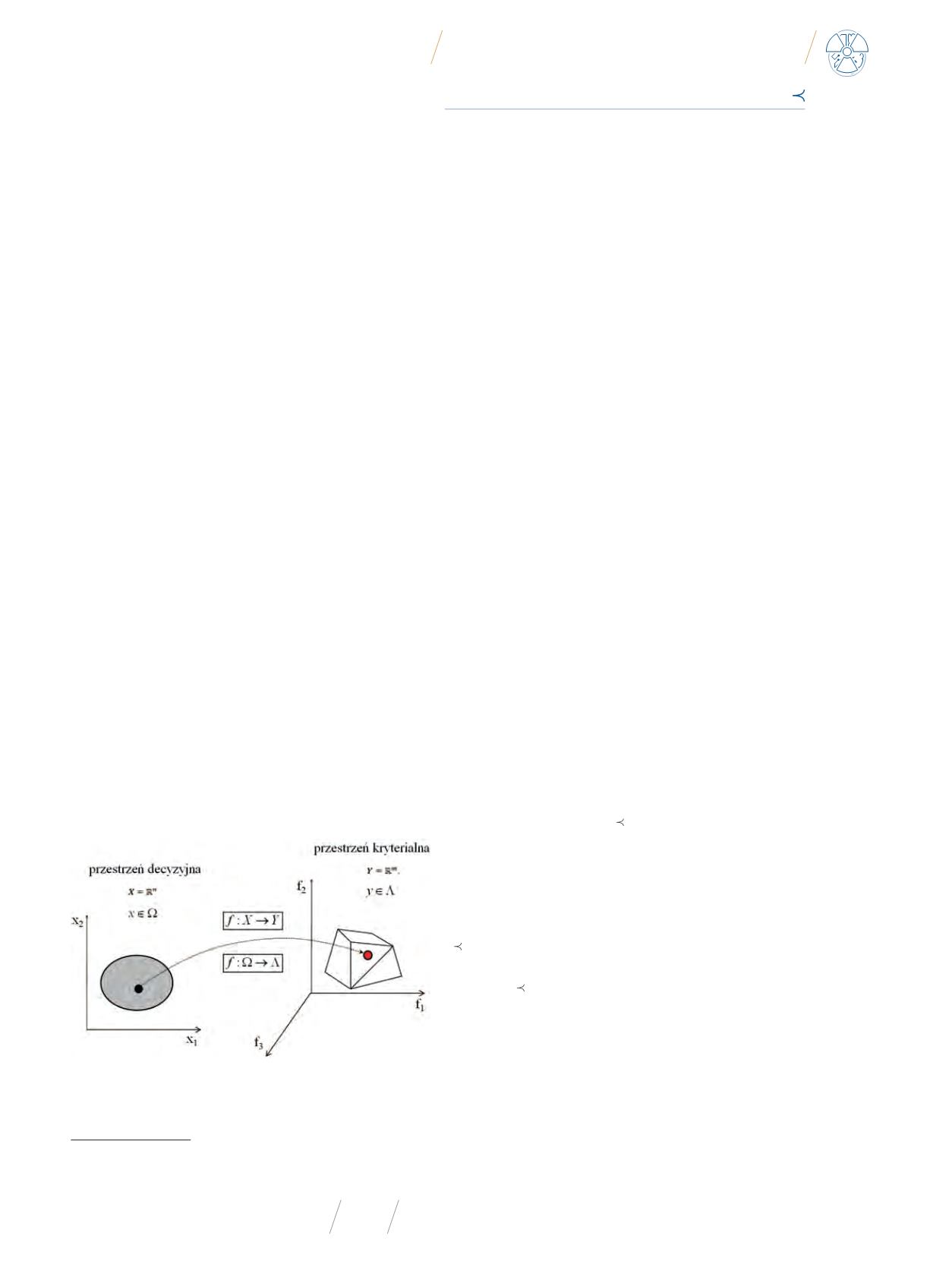
Rys. 2
Odwzorowanie przestrzeni decyzyjnej – poprzez funkcję celu – w przestrzeń
kryterialną. Każde zadanie optymalizacji wielokryterialnej może być rozpatrywane
w jednej z tych dwóch przestrzeni
Źródło: Opracowano na podstawie [17, 18].


