vol. 6 4/2017 Inżynier i Fizyk Medyczny
220
artykuł
\
article
radioterapia
\
radiotherapy
definiując rozwiązania zdominowane i niezdominowane, wpro-
wadza pewną hierarchię. To zaś bezpośrednio prowadzi do defi-
nicji Pareto-optymalności [5, 12, 14].
Definicja
Rozwiązanie (wektor zmiennych decyzyjnych)
x
∈
Ω (powiązany
z wektorem kryterialnym
y
) jest rozwiązaniem Pareto-optymal-
nym w odniesieniu do zbioru Ω wtedy i tylko wtedy, gdy nie ist-
nieje inne rozwiązanie (wektor zmiennych decyzyjnych)
x
’
∈
Ω
(powiązany z wektorem kryterialnym
y
’), dla którego wektor
x’
dominuje wektor
x
:
x
’
∈
Ω
:
x
’
x
x
’
∈
Ω
:
y
’ =
f
(
x
’) = {
f
1
(
x
’),
f
2
(
x
’),...,
f
m
(
x
’)}
y
=
f
(
x
) =
(8)
= {
f
1
(
x
),
f
2
(
x
),...,
f
m
(
x
)}
Inaczej mówiąc, nie istnieje wektor
x
’
∈
Ω, taki że:
x
’
x
⇔
[
∀
i
∈
{1,...,
m
}:
f
i
(
x
’) ≤
f
i
(
x
)]
∧
[
∃
i
∈
{1,...,
m
}:
y
i
’ <
y
i
]
(9)
z ostrą nierównością, która spełniona jest dla co najmniej jednej
wartości indeksu
i.
Jak widać, poprzez zdefiniowanie (określenie) kryteriów oce-
ny (opisane przez skalarne składowe
f
i
funkcji celu) problem
znalezienia niezdominowanych rozwiązań, czyli niezdomino-
wanych wektorów zmiennych decyzyjnych, przenoszony jest
z przestrzeni decyzyjnej do przestrzeni kryterialnej i wówczas
zagadnienie wyznaczenia najlepszej (niezdominowanej) decyzji
sprowadza się do problemu znalezienia najlepszego wektora
kryterialnego w zbiorze Λ osiągalnych wektorów kryterialnych.
W takim razie zbiór Pareto-optymalny
P
*
dla zadania optyma-
lizacji wielokryterialnej (5) to zbiór wszystkich rozwiązań (wek-
torów) Pareto-optymalnych (niezdominowanych) [10, 14, 15]:
P
* {
x
∈
Ω
|
¬∃
x
’
∈
Ω:
f
(
x
’)
f
(
x
)}
(10)
Warto zwrócić uwagę, że rozwiązania Pareto-optymalne
określane są w przestrzeni zmiennych decyzyjnych
X
. Zbiór
Pareto-optymalny odwzorowany z przestrzeni decyzyjnej
X
na
przestrzeń kryterialną
Y
ma obrazową i wyrazistą interpretację
geometryczną, tworząc w przestrzeni kryterialnej tzw.
front
Pareto
definiowany jako zbiór:
PF
{
y
=
f
(
x
) = {
f
1
(
x
),
f
2
(
x
),...,
f
m
(
x
)} |
x
∈
P
*
}
(11)
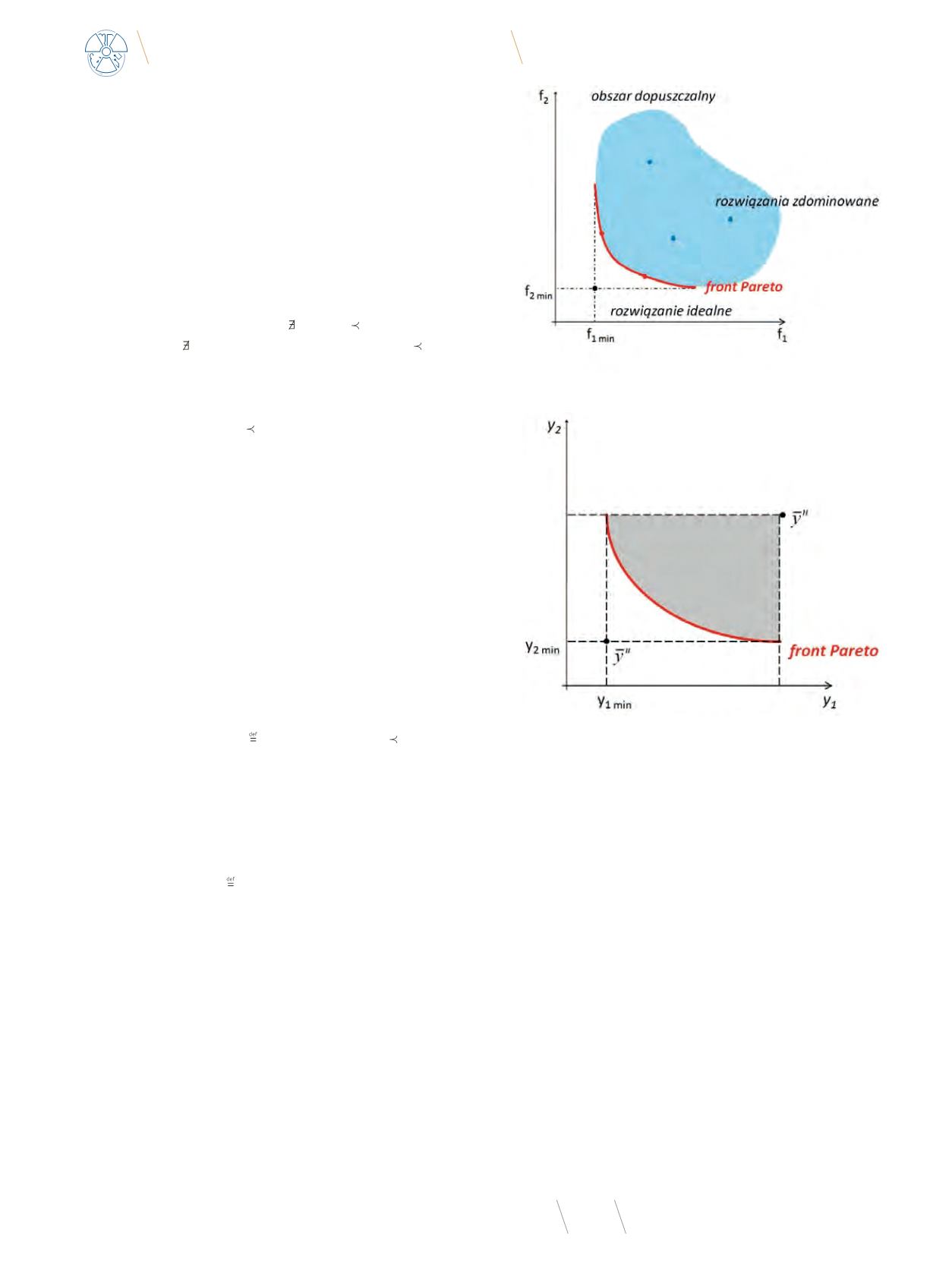
Front Pareto stanowi fragment brzegu, na którym znajdują
się rozwiązania Pareto-optymalne (niezdominowane) odwzo-
rowane w przestrzeni kryterialnej (Rys. 3). W przypadku dwu-
wymiarowej przestrzeni kryterialnej (dim
Y
=2) front Pareto jest
łatwy do wizualizacji, ponieważ stanowi on wówczas dwuwy-
miarową krzywą. Natomiast dla wymiarów wyższych niż 2 jest
on zazwyczaj nazywany
powierzchnią Pareto
.
Problem optymalizacyjny w przypadku jednokryterialnym
(znalezienie jednego najlepszego rozwiązania, czyli – inaczej
mówiąc – ocena rozwiązania z jednego tylko punktu widzenia)
jest od dawna dobrze zdefiniowany – zarówno matematycznie,
jak i algorytmicznie – a jego rozstrzygnięcie nie jest zazwyczaj
problematyczne. Sytuacja komplikuje się w znaczny sposób
Rys. 3
Interpretacja graficzna zadania optymalizacji wielokryterialnej i rozwiązań
Pareto-optymalnych w przestrzeni kryterialnej
Źródło: Opracowano na podstawie [2, 3, 4].
Rys. 4
Interpretacja graficzna problemu MCO; wektor utopii (wyrażający najlep-
sze wartości skalarnych składowych f
i
osiągane w indywidualnych – odrębnych
optymalizacjach jednokryterialnych) i wektor nadiru (reprezentujący najgorsze
wartości skalarnych składowych f
i
otrzymane w osobnych zadaniach optymalizacji
jednokryterialnej)
Źródło: [10].
w przypadku wielokryterialnym (wiele – często sprzecznych,
wzajemnie się wykluczających i trudnych do porównania – kryte-
riów oceny). Problemy dotyczą już samej fazy definiowania ma-
tematycznego danego problemu wielokryterialnego. Jeszcze
większe trudności napotyka się na etapie rozwiązywania opty-
malizacyjnego problemu wielokryterialnego.
Należy zwrócić uwagę, że definicja matematyczna problemu
optymalizacji wielokryterialnej MCO oraz jej zwięzły i prosty
zapis (5) mogą być przez tę prostotę bardzo mylące. W rzeczy-
wistości w zagadnieniach praktycznych stopień skomplikowania
zadania polegającego na wyznaczeniu optimum niestety nie
jest prostym problemem i dlatego zapisany w sposób algoryt-
miczny umożliwiający poszukiwanie rozwiązania metodami nu-
merycznymi wymaga użycia komputerów o bardzo dużej mocy
obliczeniowej. Zależy on zarówno od postaci funkcji celu (funk-
cja liniowa, wypukła, różniczkowalna itd.) – mającej albo bardzo
skomplikowaną postać analityczną, albo będącej wynikiem


